Oggi esaminiamo insieme la semiretta e il segmento, due elementi della retta, uno degli enti geometrici fondamentali, e le loro caratteristiche.
Cos’è una retta
“La retta è un insieme infinito di punti allineati nel piano e nello spazio”.
Essa è uno degli enti geometrici fondamentali, insieme al punto e al piano.
La retta non ha né un inizio né una fine, per questo si dice che sia infinita. Inoltre, essa ha una sola dimensione: la lunghezza. Non ha, invece, né profondità né altezza.
Solitamente la retta viene indicata sul piano cartesiano con la lettera r scritta in minuscolo.
Cos’è una semiretta
Se prendiamo in considerazione una retta “r” e poniamo su di essa un punto A avremo due semirette.
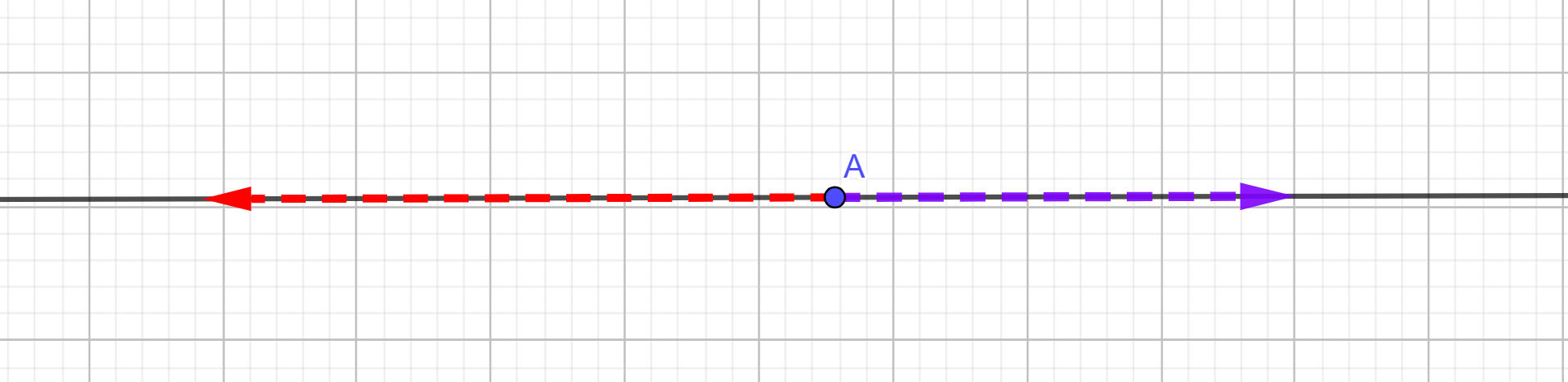
Semiretta
Esse partono entrambe dal punto A e si estendono all’infinito nella direzione opposta. Ciò rende le due semirette infinite, perché sì hanno un inizio, ma non hanno una fine.
“Si chiama semiretta ciascuna delle due parti in cui la retta viene divisa da un solo punto”.
Il punto A si dice origine della semiretta. Anche la semiretta, come la retta, ha una sola dimensione: la lunghezza.
Ogni punto, l’origine della semiretta, può essere l’inizio di infinite semirette. Ogni semiretta appartiene a un sottoinsieme della retta alla quale appartiene.
Possiamo indicare ogni semiretta con una lettera dell’alfabeto in minuscolo.
Cos’è un segmento
Se su una retta “r” poniamo due punti, anziché 1, creeremo tre sezioni diverse della retta.
La prima sezione è caratterizzata da una semiretta che parte dal punto A e si estende all’infinito, non passando per il punto B. Essa ha un inizio ma non una fine.
La seconda sezione è caratterizzata da una semiretta che parte dal punto B e si estende all’infinito, non passando per il punto A. Essa ha un inizio ma non ha una fine.
La terza sezione della nostra retta parte dal punto A e arriva al punto B. Ciò vuol dire che essa ha un inizio e una fine e per questo motivo non è una semiretta. Questa sezione della retta viene chiamata segmento.
“Il segmento è una parte finita della retta, delimitata da due punti che ne segnano l’inizio e la fine di essa”.
Possiamo utilizzare le due lettere dei punti che delimitano il segmento per indicarlo. In questo caso avremo, ad esempio, il segmento AB, delimitato dai punti A e B sulla retta r.
Segmento e figura spezzata
Ponendo due o più segmenti in modo consecutivo otteniamo una particolare figura geometrica detta figura spezzata.
Gli elementi della figura spezzata sono:
- I lati della spezzata, costituiti dai singoli segmenti.
- I vertici della spezzata, costituiti dagli estremi dei vari segmenti.
- Gli estremi della spezzata, costituiti dal primo e dall’ultimo vertice.
Una figura spezzata può essere:
- Aperta: gli estremi non coincidono.
- Chiusa: gli estremi coincidono.
- Semplice: i segmenti non si incontrano in alcun punto.
- Intrecciata: i segmenti si incontrano in altri punti oltre che agli estremi, incrociandosi.
Per indicare una figura spezzata si utilizzano le lettere in maiuscolo dei vari vertici (es: spezzata ABCD).
Segmento: confronti
Mettere a confronto due o più segmenti vuol dire vedere se essi hanno la stessa lunghezza o quali dei due ha una lunghezza maggiore o minore.
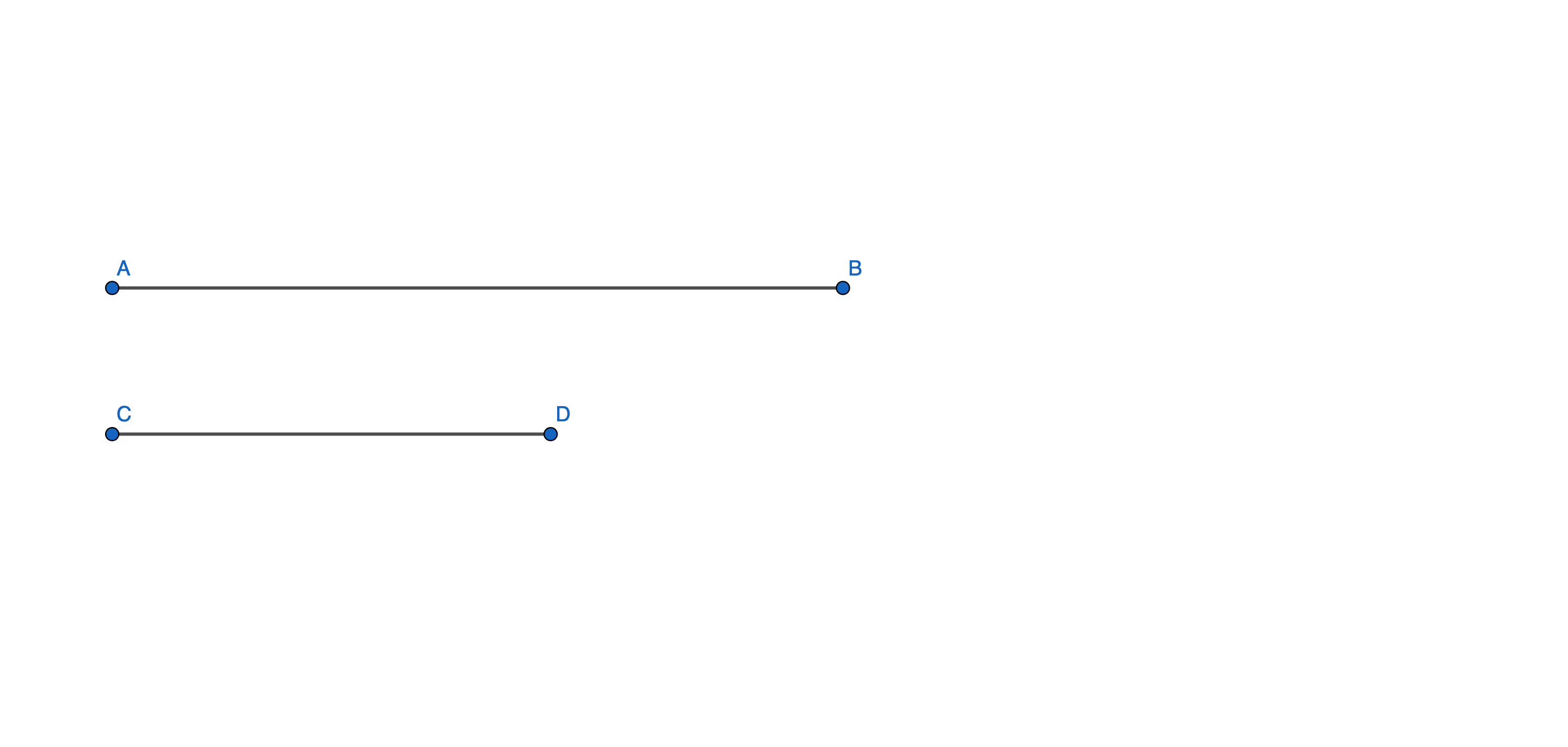
Confronto tra segmenti
Prendiamo ad esempio due segmenti che chiameremo AB e CD e proviamo a metterli a confronto. Questi possono essere i risultati:
- AB e CD hanno la stessa lunghezza, ciò vuol dire che sovrapponendo i due segmenti gli estremi coincidono. Essi si dicono congruenti. AB=CD.
- Se la lunghezza di AB è maggiore di CD si dice che il segmento AB è maggiore di CD. AB>CD.
- Se la lunghezza di AB è minore di CD si dice che il segmento AB è minore di CD. AB<CD.








