Alla base della geometria ci sono i tre enti geometrici fondamentali: il punto, la retta e il piano. Il matematico greco Euclide, dal quale discende tutto lo studio della geometria, fondò lo studio di quest’ultima su questi tre enti.
Di cosa si occupa la geometria
Per capire meglio di cosa si occupa la geometria dovremmo innanzitutto esaminare bene l’etimologia della parola stessa.
La parola geometria, infatti, è composta da due parole greche: geo, che vuol dire terra o terreno, e metria, che vuol dire misura. Geometria è, quindi, la misurazione della terra.
“La geometria è quella parte della matematica che si occupa delle forme nel piano e nello spazio, e delle loro mutue relazioni” – Wikipedia.
La geometria Euclidea
La geometria base che conosciamo e studiamo discende dal grande matematico greco Euclide e, per questo, viene anche chiamata geometria Euclidea.
Euclide fondò lo studio di tutta la geometria sui tre enti geometrici fondamentali: il punto, la retta e il piano.
Lo scopo della geometria euclidea è quello di rappresentare la realtà e tutti gli oggetti nello spazio tridimensionale nel quale viviamo.
Geometria piana e geometria solida
Possiamo dividere la geometria in geometria piana e geometria solida.
La geometria piana si occupa di rappresentare le figure sul piano. Essa parte dall’ente geometrico fondamentale della retta, con la quale vengono costruiti i segmenti che a loro volta formano i poligoni (triangolo, quadrato, pentagono, esagono, ecc).
La geometria solida, invece, studia le costruzioni geometriche nello spazio. Utilizzando i segmenti e i poligoni è possibile costruire i poliedri (il cubo, la piramide, ecc).
Gli enti geometrici fondamentali
Come detto, gli enti geometrici fondamentali sui quali Euclide basa tutto il suo studio della geometria sono tre: il punto, la retta e il piano.
Questi tre enti non sono definibili ma sono tutti comprensibili.
Il punto
Il primo ente geometrico fondamentale è il punto. Esso è un concetto primitivo privo di alcuna definizione.
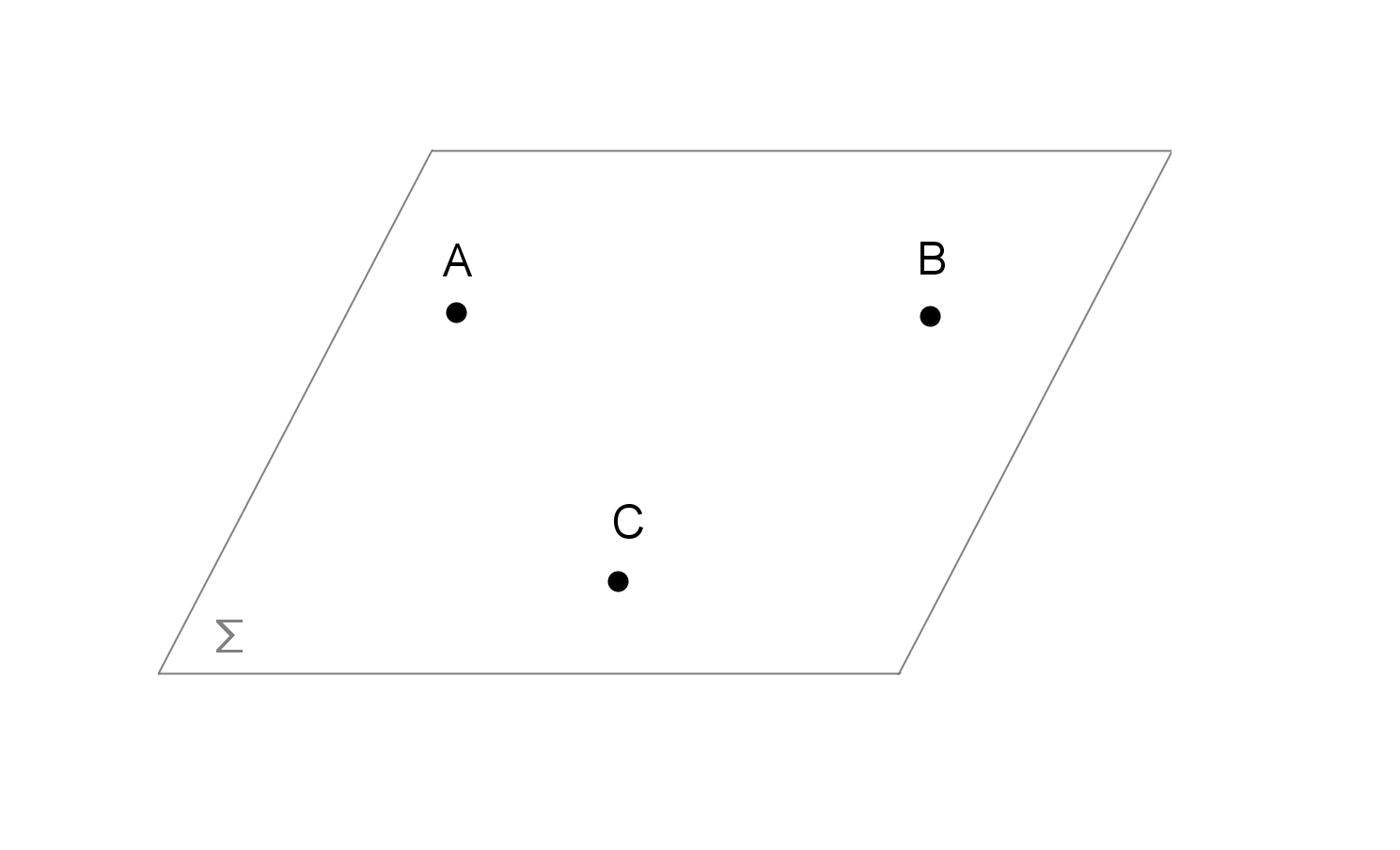
Punto
Non ha nessuna dimensione, ma indica solamente una posizione nello spazio. Il punto si scrive utilizzando una lettera dell’alfabeto scritta in maiuscolo (es: A).
La matematica euclidea prova a spiegare il concetto di punto che, sebbene sia indefinibile è comprensibile. Una stella in un cielo notturno, il segno di una matita su un foglio bianco o la punta di uno spillo.
Gli enti geometrici fondamentali: la retta
Il secondo ente geometrico fondamentale è la retta. Esso è composto da un insieme infinito di punti l’uno attaccato all’altro aventi sempre la stessa direzione.
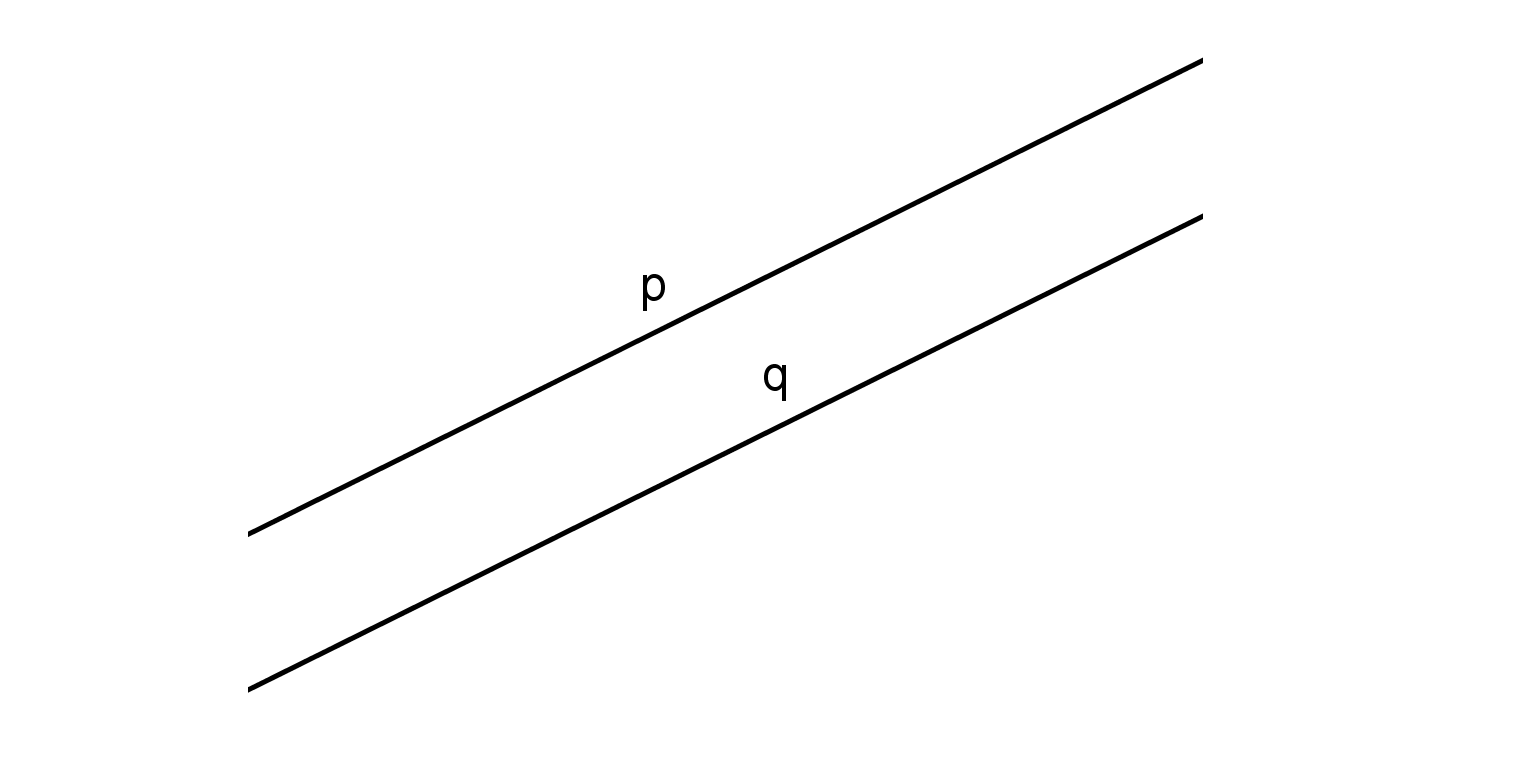
La retta
Essa ha una sola dimensione: la lunghezza. La retta viene indicata utilizzando una lettera dell’alfabeto scritta in minuscolo (es: a).
La retta è priva di spessore e infinita, ovvero la sua lunghezza è illimitata sia in una direzione che nell’altra. Possiamo immaginarla visivamente come il segno di lasciato da una matita che scorre su un foglio bianco.
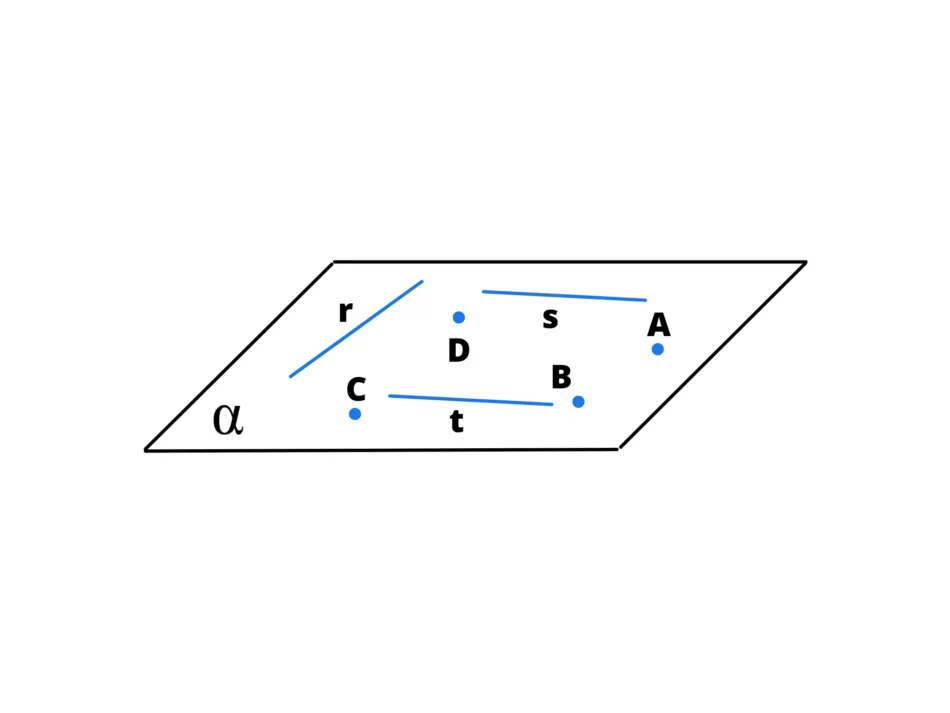
Gli enti geometrici fondamentali: il piano
Il terzo e ultimo ente geometrico fondamentale è il piano. Esso è composto da un insieme infinito di rette l’una attaccata all’altra.
Esso ha due dimensioni: la lunghezza e la larghezza. Il piano viene indicato utilizzando una lettera dell’alfabeto greco scritta in minuscolo: α (alfa), β (beta).
Possiamo immaginare il piano visivamente come un foglio di carta bianco, il pavimento di una stanza, il piano di un tavolo.