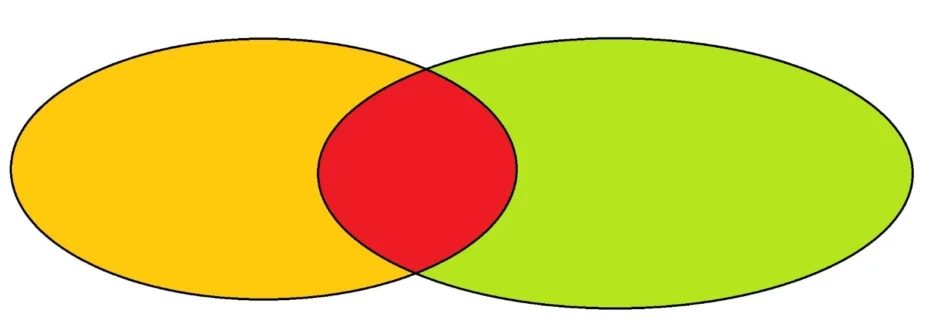
Con il termine insieme si indica un gruppo di cose, persone o animali che hanno una caratteristica in comune e che rappresentano gli elementi degli insiemi stessi.
La teoria degli insiemi
Gli insiemi vengono utilizzati in matematica per raggruppare persone, animali o cose con una caratteristica comune. Possiamo ad esempio raggruppare nell’insieme dei numeri pari il 2, il 4, il 6, ecc.
Insiemi
Un insieme si identifica con le lettere maiuscole (A, B, C, ecc), mentre i suoi elementi si indentificano con le lettere minuscole (a, b, c, ecc).
Spesso per indicare un insieme si utilizzano anche le parentesi graffe. Es: A {a, b, c}.
Rappresentazione degli insiemi
Gli insiemi possono essere rappresentati in tre modi diversi:
- Elencazione o tabulare: è un metodo utilizzato principalmente quando gli elementi sono pochi e consiste nell’elencare gli elementi e racchiuderli fra parentesi graffe e separandoli con una virgola. Es: insieme delle vocali A= {a, e, i, o, u}.
- Caratteristica: si raggruppano gli elementi in base a una caratteristica comune. Si utilizza quando gli elementi sono numerosi.
- Diagramma di Eurelo-Venn: è la rappresentazione grafica dell’insieme. Si disegna un ovale con al suo interno tanti puntini quanti sono gli elementi da inserire e accanto ad essi si scrive il nome dell’elemento stesso.
Sottoinsiemi
In alcune rappresentazioni i sottoinsiemi sono indispensabili. “Si definisce B sottoinsieme di A se ogni elemento di B appartiene anche ad A, ma c’è almeno un elemento di A che non è presente a B”.
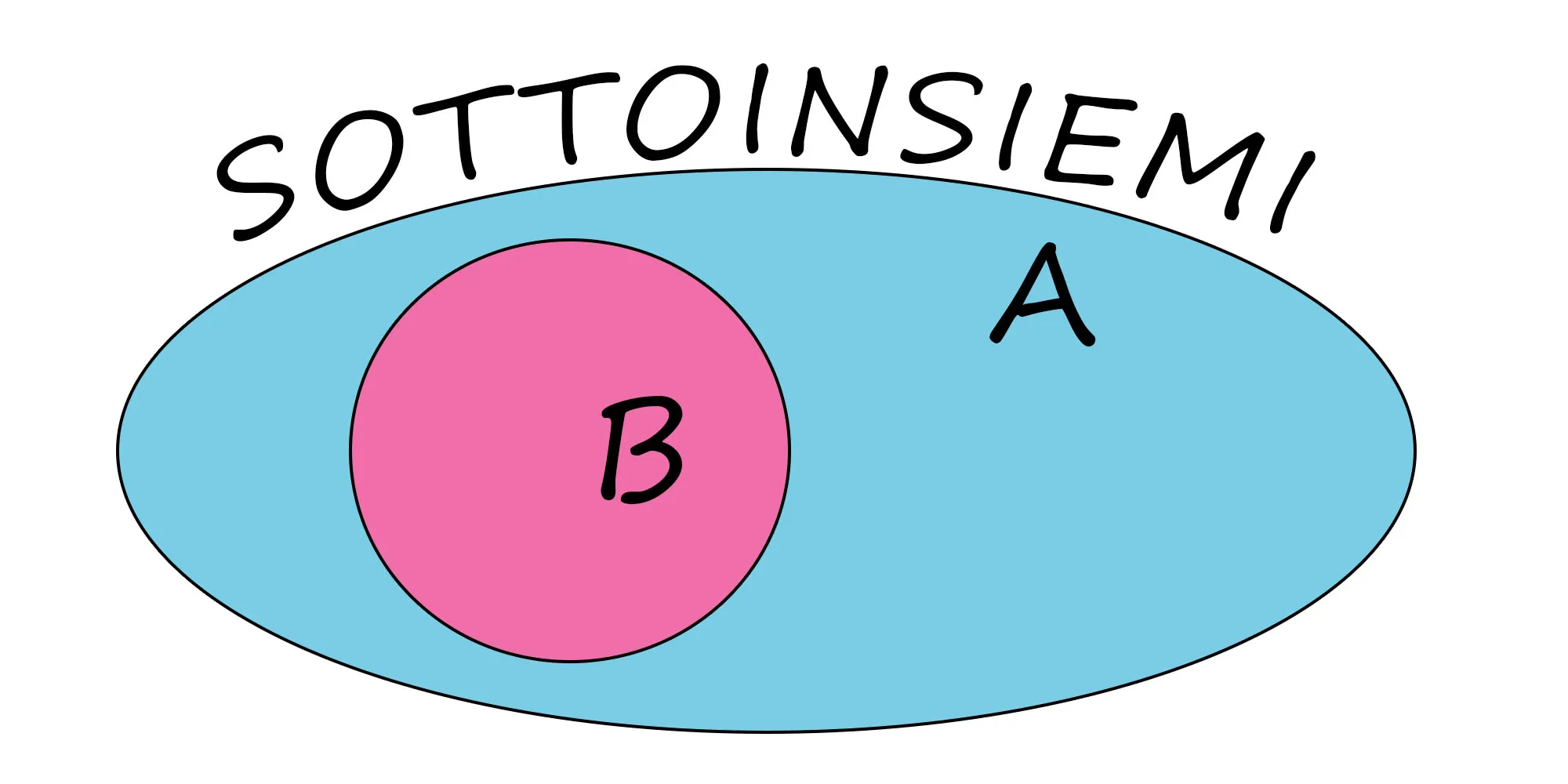
Sottoinsieme
Insiemi particolari
Possono esserci categorie particolari di insiemi:
- Finito e infinito: si dice finito un insieme con al suo interno un numero finito di elementi. Ad esempio, l’insieme delle vocali dell’alfabeto italiano. Si dice infinito un insieme con al suo interno un numero infinito di elementi. Ad esempio, l’insieme di tutti i numeri pari.
- Vuoto: un insieme si dice vuoto quando non possono esserci elementi al suo interno. Ad esempio, l’insieme dei mesi dell’anno con 32 giorni.
- Unitario: un insieme si dice unitario quando è formato da un solo elemento. Ad esempio, l’insieme dei mesi dell’anno che hanno meno di 30 giorni.
Le operazioni
Le operazioni con gli insiemi sono due:
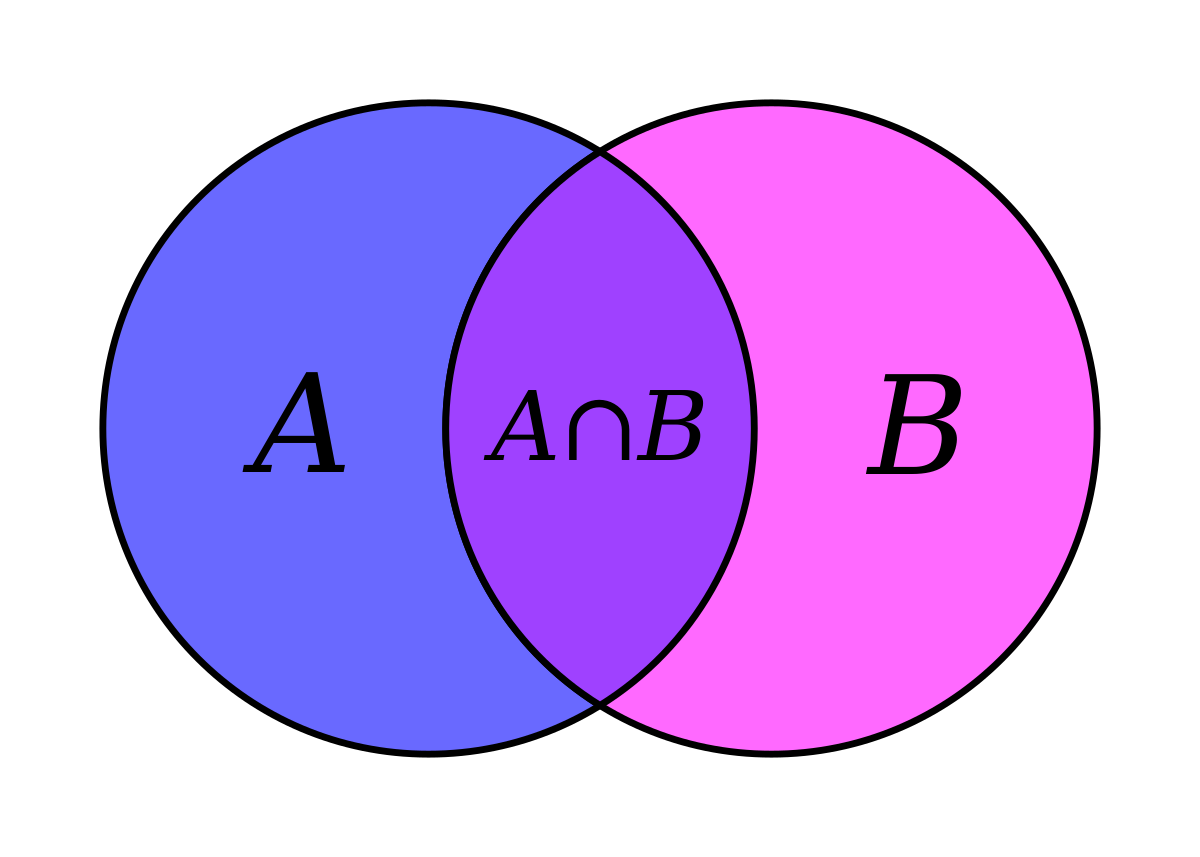
- Intersezione: si dice intersezione l’insieme che contiene gli elementi che appartengono sia all’insieme A che all’insieme B. Es: A= {p, a, n, e}; B= {m, a, r, e}; intersezione= {a, e}.
- Unione: l’unione è l’insieme con tutti gli elementi che appartengono sia all’insieme A che B, senza ripetere gli elementi uguali. Es: A= {m, a, r, e}; B= {p, a, n, e}; unione= {m, a, r, e, p, n}.
Se due insiemi non hanno alcun elemento in comune si dicono disgiunti.
Le proprietà
Le proprietà delle due operazioni degli insiemi sono:
- Proprietà commutativa.
- Proprietà associativa.
- Proprietà dell’insieme vuoto.
- Proprietà distributiva.
Insieme universo
L’insieme universo, anche detto insieme ambiente, è complementare all’insieme vuoto. Esso contiene tutti gli insiemi, che sono suoi sottoinsiemi. Fanno parte dei suoi sottoinsiemi tutti gli insiemi, compreso l’insieme vuoto e sé stesso.
Insieme
Graficamente viene rappresentato con un triangolo all’interno del quale sono contenuti tutti gli insiemi.
Insieme differenza
L’insieme differenza contiene tutti gli elementi che appartengono all’insieme A ma non appartengono all’insieme B.
Es: A= {5, 6, 7, 8, 9}; B= {2, 3, 4, 5, 6}; insieme differenza A-B= {7, 8, 9}.
Insieme complementare
L’insieme complementare è la differenza tra l’insieme a e il sottoinsieme B.
Es: A= {1, 2, 3, 4}; B= {1, 2}; insieme differenza A-B= {3, 4}.
Insiemi delle parti
L’insieme delle parti è formato da tutti i sottoinsiemi propri e impropri dell’insieme A.
I sottoinsiemi impropri di A sono l’insieme vuoto e A stesso.